 Op een kermis moet het grondoppervlak van een paardjesmolen herschilderd worden. Omdat dit met een uiterste dure verf dient te gebeuren, is het absoluut noodzakelijk het exact oppervlak te kennen.
Op een kermis moet het grondoppervlak van een paardjesmolen herschilderd worden. Omdat dit met een uiterste dure verf dient te gebeuren, is het absoluut noodzakelijk het exact oppervlak te kennen.
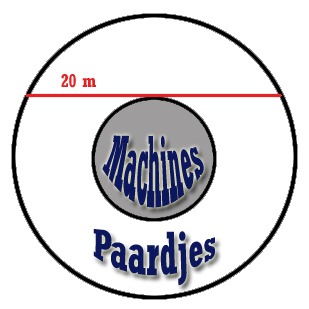
Het oppervlak is uiteraard dat waar de paardjes staan. De ruimte waar de machines staan, dient niet mee geschilderd te worden. Het te herschilderen oppervlak wordt dus bepaald door twee cirkels met het zelfde middelpunt (zoals aangegeven in het plaatje).
De uitbater van de paardjesmolen zit nu met de handen in het haar. Het enige wat hij heeft kunnen opmeten is de lengte van een koord – tussen twee punten op de buitenste cirkel – die de binnenste cirkel net raakt. Die lengte bedraagt 20 meter.
Is dat voldoende om het gezochte oppervlak te berekenen? Waar zitten de wiskundigen onder de “intussen… BLOG”-lezers. Kruip uit uw schulp!
Peter

De paardjescirkel > de verfcirkel > de machinecirkel en 10m is de cotangens van de verfcirkel. Ook al mocht ik het bij het rechte eind hebben, dan betwijfel ik dat de uitbater de juiste hoeveelheid verf koopt.
Intuitief geredeneerd zou ik zeggen 314m². De gemeten lijn van 20m is de middelijn van de cirkel die de oppervlakte heeft gelijk aan de opppervlakte van de totale paardjesmolen min de cirkel van het machinegedeelte. dus 10x10x3,14 is 314m²
‘k zou zeggen op het eerste zicht Pi * (20/2)² , of 314 m²
opp buitenste – opp binnenste
R² = 10² + r² en Opp = pi * (R²-r²)
Grtjs, Rudy
Amai Jan en Rudy, dat is vlug gevonden.
Ik werk het wel even uit:
De stelling van Pythagoras leert ons dat :
R² = 10² + r² (waarbij “R” staat voor straal buitenste cirkel en “r” voor straal binnenste cirkel).
en dus : Pi*R² = Pi*(10² + r²)
en dus : Pi*R² = Pi*10² + Pi*r²
en dus : Pi*R² – Pi*r² = Pi*10²
en dus : opp. buitenste cirkel – opp. binnenste cirkel = 3.14*100
en dus : te herschilderen oppervlak = 314 m²